The Billionaire Bet: Quantum Computing
Quantum stocks like IonQ and Rigetti are soaring in 2024 but is this just hype or a real tech revolution?
Dominik Andrzejczuk
Dec 30, 2024 - 11:56 AM

The Original Article, written in Polish by: Paweł Gora, Sebastian Zając, Przemysław Michałowski, Krzysztof Kuba in cooperation with the Quantum AI Foundation.
Quantum computing stocks, including IonQ (NYSE:IONQ) and Rigetti (NYSE:RGTI), have surged dramatically this year, fueled in part by the buzz surrounding Google’s new quantum chip, Willow. Touted for its unprecedented speed and improved error-correction capabilities, Willow sparks both hope and caution: while it paves the way for breakthrough technologies, it also raises concerns about future threats to cryptocurrency security. Despite Google’s insistence that such a threat remains a decade away, this latest leap forward has investors and innovators alike rethinking the immense potential, and possible perils, of quantum computing.
But what exactly is Quantum Computing, or Quantum Technologies in general? And how are these groundbreaking technologies going to affect us?
A Brief History of Quantum Mechanics
In the late 19th and early 20th centuries, two key physical theories—classical mechanics and electrodynamics—appeared to explain most of the known phenomena at that time. But there was one puzzling observation that simply didn’t fit these existing theories: the strange behavior of blackbody radiation. In 1900, Max Planck introduced the concept of energy quantization to explain this anomaly, opening the door to a genuine revolution in physics [1].
These new quantum ideas quickly gained acceptance and were embraced by leading scientists, including Albert Einstein (investigating the photoelectric effect [2]), Niels Bohr (proposing the hydrogen atom model [3]), Louis de Broglie (introducing wave-particle duality [4]), Werner Heisenberg (developing matrix mechanics [5]), and Erwin Schrödinger (formulating wave mechanics based on the wave function [6]). Their collective efforts shaped the new quantum theories describing the microscopic world.
Since then, quantum mechanics has revolutionized our understanding of physical theories and paved the way for quantum technologies. Beyond the introduction of energy quantization, quantum theory has helped us make sense of atomic structure and the processes happening inside stars, and it has driven the development of breakthroughs like electron microscopes, laser technology, research on superconductivity, and the study of elementary particles. It turns out that so-called “classical” physics is merely a special case of quantum mechanics [7].
Modern physics goes even further by combining special relativity with quantum mechanics in what is known as “quantum field theory,” describing the fundamental interactions between elementary particles [8]. Researchers are also exploring multi-dimensional objects [9, 10], although we still lack a complete understanding of “quantum gravity” [11], which aims to unify quantum mechanics with general relativity. There remain many unanswered questions waiting for new discoveries. It’s an exciting time for physics—full of surprises and potential breakthroughs.
Quantum mechanics itself is a fascinating but sometimes perplexing world, expressed through a variety of mathematical principles. Even seasoned physicists can find these rules hard to grasp. One of the most famous paradoxes intended to highlight the puzzling nature of quantum mechanics was introduced in 1935 by Albert Einstein, Boris Podolsky, and Nathan Rosen—the EPR paradox [12]. They argued that so-called entangled states (predicted by quantum mechanics) would imply instantaneous communication, conflicting with the rule that nothing can travel faster than the speed of light.
In 1964, John Bell proposed what is now known as Bell’s theorem, showing that no classical theory consistent with relativity can match the predictions of quantum mechanics for entangled states [13]. This opened the door to new lines of research and became a cornerstone of quantum information science. Numerous experiments (including one of the first by Alain Aspect [14]) confirmed the absence of “hidden variables” that would act like unmeasured classical properties explaining experimental results. In subsequent years, Simon Kochen and Ernst Specker developed a theory ruling out many interpretations of quantum mechanics based on realism [15], and these too were experimentally confirmed.
In the 1980s, researchers also considered the possibility of using quantum effects to transmit information faster than light. This prompted the formulation of the no-cloning theorem [16], an early breakthrough in quantum information theory that recognized the theoretical possibilities of storing and processing information using quantum rules. Over time, quantum theory has profoundly influenced technology, enabling the manipulation of single atoms in magnetic traps and the advancement of scanning electron microscopes. These achievements laid the foundations for today’s qubit-based processors, the fundamental units of quantum computing.
The Dawn of Quantum Computing
Our modern world would be unrecognizable without machines capable of analyzing, simulating, and optimizing solutions to highly complex computational problems—even generating text, images, video, or computer code. Although computers’ shapes and sizes keep evolving, their operation still relies on the theoretical frameworks suggested by Alan Turing and John von Neumann. In 1936, Turing described the “Turing machine,” which became a cornerstone of theoretical computer science and clarified which problems could be solved by such a machine [17]. Von Neumann later proposed the computer architecture that underpins the computers we use today [18].
Quantum information science (in line with quantum information theory) offers an entirely new model of information processing—leveraging the principles of quantum mechanics to tackle computational problems. The fascinating history of quantum computing also features a few notable Polish contributions. In 1976, Polish physicist Roman Stanisław Ingarden published a fundamental formulation of quantum information theory, earning him recognition as one of its founding fathers [19]. Three years later, in 1979, Paul Benioff proposed the quantum Turing machine model, which would solve problems using the laws of quantum mechanics [20].
Many cite Richard Feynman’s 1981 presentation as the birth of quantum computing, in which he proposed using quantum computers to simulate quantum phenomena [21]. Feynman’s insight was that quantum machines could model the behavior of particles at the microscopic level far more efficiently than classical computers, which would need enormous time to complete such simulations.
In 1992, David Deutsch introduced the first quantum algorithm that could solve certain computational problems faster than a classical machine [22]. This inspired further research into quantum algorithms, ultimately paving the way for the future of quantum computers. By the 1990s, the first experiments aimed at physical implementations of quantum computers appeared. Researchers built early prototypes that harnessed quantum effects to process information. In 2001, an experiment demonstrated quantum teleportation of information, offering practical proof that the principles of quantum mechanics could securely transmit data between distant locations.
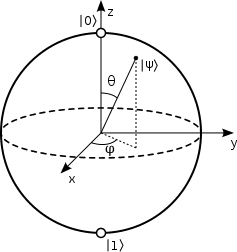
To better appreciate quantum computers’ potential, it helps to look at how they handle computations. In traditional computers, the smallest unit of information is a bit (short for “binary digit”), which can be in one of two basic states—usually labeled 0 or 1—much like two distinct points on a line. By contrast, the quantum counterpart, called a qubit, can be seen as a point on a sphere known as the Bloch sphere (Figure 1). The “north” and “south” poles of the Bloch sphere represent the 0 and 1 states, but all other points correspond to quantum states in what we call a superposition. These superposition states carry information about both 0 and 1, enabling quantum devices to operate on many states at once—an incredible feature that underlies the parallel processing power in quantum computing.
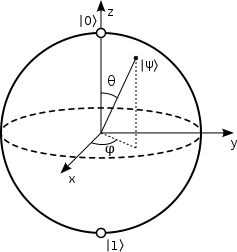
Superposition can be tricky for newcomers to quantum mechanics, mostly because we don’t observe it directly in the everyday, “classical” world. Why? Although we can create a qubit in a superposition of 0 and 1, we can’t measure it in that state directly: as soon as we measure the qubit, it collapses into one of the two basis states (0 or 1). The likelihood of getting either 0 or 1 depends on the state the qubit was in before the measurement. On one hand, this implies that the outputs of quantum calculations can be probabilistic. On the other, it’s precisely this feature that allows a quantum computer to explore all possible values at once, rather than checking them one by one as a classical computer would.
To change a qubit’s state, we use quantum gates. In classical computing, we operate on bits by sending electrical signals through transistors and logic gates such as AND, OR, and NOT. In quantum computing, the gates are represented by unitary matrices that act on qubits (represented mathematically as vectors) without changing their magnitude. Examples include the Hadamard gate or the CNOT gate. Applying these gates to qubits in superposition creates new superpositions, letting us “tune” the probability of measuring 0 or 1 [23].
Besides superposition, there’s another quantum phenomenon that can feel counterintuitive even to advanced scientists: quantum entanglement. This was famously labeled “spooky action at a distance” by Albert Einstein [24]. Entanglement refers to a special relationship between two or more quantum objects—such as photons or qubits—where you can’t fully describe the state of one object without accounting for the state of the other(s). In practice, that means a measurement on one entangled particle instantly influences the outcomes of measurements performed on the others, regardless of how far apart they may be. In quantum computing, the measurement outcome of one qubit in an entangled system immediately affects the measurement results of the other qubits—something with no analog in classical physics or conventional computing.
Although practical quantum computers only came along decades later, scientists had already been developing quantum algorithms designed to run on these future machines. Early examples include Deutsch’s algorithm [25] (1985), the Bernstein–Vazirani algorithm [26] (1993), and Simon’s algorithm [27] (1994). These didn’t necessarily solve real-world problems but proved that quantum algorithms can, in fact, be faster than classical ones, thanks to superposition and entanglement.
A groundbreaking development came in 1994 when Peter Shor introduced a polynomial-time quantum algorithm for factoring large numbers [28, 29]. This was dramatically faster than any known classical approach. While it hasn’t been definitively proven that a classical computer can’t match this speed, the consensus is that factoring large numbers using classical methods is vastly more time-consuming. Since the difficulty of factoring large numbers underpins today’s cryptographic systems (like RSA [30]), the arrival of powerful quantum computers could force us to rethink encryption. Research is already underway in many countries, including Poland, to develop “post-quantum” cryptographic algorithms that would remain secure in the face of quantum attacks [31].
Building Quantum Computers
Classical computers—whether desktops, tablets, or smartphones—rely on ongoing miniaturization and the use of transistors and integrated circuits to carry out their computations. According to Moore’s Law, the number of transistors we can pack onto a chip doubles roughly every two years, and modern chips can host billions of components. Yet some computational tasks remain too large even for today’s supercomputers, which operate at the scale of petaflops (10^15 floating-point operations per second). For certain problems—such as complex material simulations, modeling quantum systems, or tackling sophisticated optimization tasks—the required computing time balloons exponentially with the size of the input, rendering these problems effectively unsolvable on a classical machine.
Moreover, as transistor sizes shrink further, Moore’s Law is expected to hit fundamental limits, partly due to quantum effects at very small scales. That’s why scientists began searching for alternatives, suspecting that quantum mechanics might bring a leap forward. Quantum parallelism—operating on multiple states at once—could theoretically offer a massive speed boost.
The first quantum computer is often credited to Isaac Chuang, Neil Gershenfeld, and Mark Kubinec in 1998 [32]. It had only two qubits and suffered from rapid decoherence (the transition from quantum to classical behavior), which caused information loss. While it wasn’t powerful enough for complex calculations, it did demonstrate that quantum-based computation was possible. Their approach differed from modern quantum computing methods: instead of controlling single atoms, they chose to work with a large ensemble. They used organic chloroform (CHCl3) molecules. In a strong magnetic field, the nuclear spins of carbon and hydrogen atoms can be aligned or opposed to the field’s direction—essentially a 1 or a 0. To flip the spin, you apply a radio-frequency electromagnetic pulse. It’s noteworthy they had to use the C-13 isotope of carbon for its magnetic properties. Spin is an intrinsic quantum property with no direct analog in our everyday world.
Today’s quantum computers [33] use similar quantum phenomena but are constructed differently. Three of the most common qubit technologies are trapped ions [34], superconducting circuits [35], and photon polarization [36]. Regardless of the chosen approach, these computers must be kept at extremely low temperatures—close to absolute zero—and at very low pressure. The cold suppresses unwanted molecular vibrations, while the near-vacuum environment reduces the risk that stray particles will collide with qubits and introduce errors. This is why photographs of quantum computers often show them hanging upside down (Figure 2) with a maze of cables descending from them; those cables and components provide the cryogenic environment and ensure stable conditions for computation.

Let’s talk about the first of these technologies: trapped ions. This method ionizes an atom by removing one electron, creating a positively charged ion that interacts with an external electromagnetic field. By carefully configuring that field, scientists can trap the ion in a specific location in space. An array of around 100 miniature electrodes arranges these ions (qubits) in a line, allowing them to interact in a controlled way. Lasers are then used to manipulate qubits and implement quantum gates to achieve superposition and entanglement. Companies like IonQ [37], AQT [38], Oxford Ionics [39], and Quantinuum [40] use this trapped-ion approach.
Another popular platform relies on superconducting qubits—materials that, at near-zero temperatures, have zero electrical resistance. A superconducting circuit made from a capacitor and a Josephson junction (which harnesses quantum tunneling) forms the core of a qubit. An external capacitor enables communication with the outside world and helps create quantum entanglement. Tech giants such as Google [41], IBM [42], and Rigetti [43] have built superconducting quantum processors.
A third method encodes qubits in photons, leveraging properties like photon polarization. Companies like Xanadu [44] and PsiQuantum [45] use lasers, lenses, polarizers, and beam splitters to implement their quantum gates in optical setups.
Additionally, there’s the concept of quantum annealing [46], primarily used for combinatorial optimization and sampling problems [47]. This technique involves formulating the problem as minimizing the energy of a qubit system. Once you encode your data and start the annealing process, the system “settles” into a low-energy configuration that corresponds to a solution. The result may be probabilistic. Unlike universal quantum computers, quantum annealers don’t rely on quantum gates. D-Wave is a pioneer of this approach, employing superconducting qubits whose states are manipulated via magnetic fields [48].
Beyond these, other emerging quantum computing technologies include topological qubits, semiconductor approaches, and silicon-based methods.
Applications of Quantum Computing
Quantum computing has enormous potential in a wide variety of fields. In areas where rapid response is critical—for instance, high-frequency trading—quantum algorithms could yield a competitive edge. Meanwhile, pharmaceutical and materials engineering could benefit from Feynman’s original dream: using quantum simulations to develop new drugs and materials. Quantum algorithms for optimization could transform logistics, finance, and energy network design. In 2017, researchers at D-Wave and Volkswagen published a study demonstrating how to optimize taxi fleet routing through quantum annealing [49].
Quantum computing also underpins “quantum machine learning” (QML), which explores how quantum mechanics might speed up and enhance machine learning algorithms. Quantum ML uses qubits and superposition to build more efficient models for tasks like data analysis or solving difficult optimization problems—such as automating the search for the best hyperparameters. This intriguing fusion of quantum theory and data processing holds vast promise for new kinds of technology. Some researchers have even demonstrated how quantum algorithms can boost classical machine-learning models for satellite image object detection.
Quantum devices can also help sample from probability distributions (like the Boltzmann distribution [50]) that are challenging to handle on classical machines. And there are even artistic applications: using quantum computers to generate music [51]!
These days, companies like IBM, Google, and Rigetti offer cloud-based access to quantum processors. While we’re witnessing an exciting time for quantum computing, there are still significant scientific and engineering challenges to overcome, such as maintaining and stabilizing qubits and protecting quantum information against noise. Present-day machines often produce “noisy” results, and decoherence remains a major obstacle to reliably preserving qubit states long enough for useful computation.
Other Quantum Technologies
Long before the first quantum computers existed, Charles Bennett and Gilles Brassard demonstrated in 1984 that quantum physics could enable secure communication [52]. Their method exploited the polarization of photons. By measuring photon polarization, communicators could not only exchange messages but also detect eavesdropping attempts. This formed the basis of quantum cryptography, and in practice, these ideas are mostly applied to quantum key distribution (QKD), where the actual (classical) message is encrypted with a key established via quantum methods. Artur Ekert, a Polish physicist and professor at Oxford, built on Bell’s theorem to propose an entanglement-based approach for secure communication [53], for which he recently received the Milner Award from the Royal Society in the UK [54]. QKD is already being tested in many places— for instance, as part of the NLPQT (National Laboratory for Photonics and Quantum Technologies) project, a QKD transmission link has been established between Poznań and Warsaw across 380 km of dedicated PIONIER network fibers [55].
Quantum technologies can also help make ultra-precise measurements, a field known as quantum metrology [56]. For example, atomic clocks rely on quantum effects within atomic oscillations, allowing them to keep time far more accurately than standard clocks. Quantum interferometry leverages the interference of quantum states (where two or more states combine, adding or subtracting their amplitudes to create a new state) to measure distances, positions, and tiny movements with exquisite precision. Quantum spectroscopy examines the energy levels of atoms and molecules, essential for studying a substance’s properties and composition.
The Quantum Technology Ecosystem in Poland
Although quantum technologies are still developing, they already show massive economic and industrial potential. Polish scientists have played—and continue to play—a key role in quantum information science. For instance, the no-cloning theorem [57], Ekert’s entanglement-based QKD protocol (E91) [53], and the GKS-L equation [58] all highlight significant Polish contributions to the foundation of quantum mechanics and quantum information.
In Poland, numerous research groups focus on quantum technologies, and there are startups and companies advancing R&D or building quantum-tech products. There’s even a Quantum Cluster [59] aiming to cultivate Poland’s capacity in these fields, as well as an ambitious effort in Poznań to construct one of the first quantum computers in the European Union as part of the EuroHPC program [60].
QPoland [61] is one of the organizations supporting the Polish quantum computing community, and the authors of this article are members of that group. QPoland unites researchers from multiple Polish universities and companies under the international QWorld [62] initiative. Formally, QPoland is supported by the Quantum AI Foundation [63], whose mission is to bolster education, research, and collaboration in science and emerging technologies. Together, the foundation and QPoland host free lectures, meetups, workshops, conferences, and competitions related to quantum technologies—often in collaboration with experts from other countries. These events are opportunities for anyone interested in quantum tech to gain skills, share knowledge, and make valuable connections.
A more detailed overview of Poland’s quantum technology ecosystem will be published in a few months. In the meantime, you might consider joining some of the upcoming remote, free workshops on quantum programming [64] or the third edition of the international Quantum Games Hackathon [65], organized by the Quantum AI Foundation from September 30 to October 8. Participants from around the globe will collaborate virtually to develop new quantum-themed games. The hackathon begins with workshops designed to teach the basics of writing code that can run on real quantum computers. Participants can then test their knowledge with a quiz and earn a certificate.
References
[1] M. Planck, “On the Theory of the Energy Distribution Law of the Normal Spectrum”. Verhandl. Dtsch. phys. Ges. 2, 237 (1900).
[2] A. Einstein, “Uber einen die Erzeugung und Verwandlung des Lichtes, Annalen der Physik 4, (1905).
[3] N. Bohr Dr. phil. I. On the construction of atoms and molecules. Philosophical Magazine Series 6, 2, (1913).
[4] L. de Broglie,Waves and quanta, Nature. 112 2815: 540 (1923).
[5] M. Born, W. Heisenberg, P. Jordan, Zur Quantenmechanik II, Zeitschrift fur Physik, 35, 557–615, (1925).
[6] E. Schrodinger, The Present Status of Quantum Mechanics, Die Naturwissenschaften, Volume 23, Issue 48, (1935).
[7] D. Griffits, D. Schroeter, Wstęp do Mechaniki Kwantowej, PWN, (2021).
[8] S. Weinberg, The Quantum Theory of Fields, Cambridge University Press; First Edition, (2005).
[9] B. Zwiebach, A First Course in String Theory, Cambridge University Press; (2004).
[10] M. Green, J. Schwarz, E. Witten, Superstring Theory. Cambridge
University Press, Cambridge, UK, (1987).
[11] C. Rovelli, Quantum Gravity, Cambridge University Press, UK, (2004).
[12] A. Einstein, B Podolsky, N Rosen, Can Quantum-Mechanical Description of Physical Reality be Considered Complete?, Physical Review. 47 (10) 777–780, (1935).
[13] J. Bell, On The Einstein Podolsky Rosen Paradox, Physics 1, 195–200,
(1964).
[14] A. Aspect, Proposed experiment to test the nonseparability of
quantum mechanics. PhysRevD vol 14 no 8.p 1944–1951, (1976).
[15] S. Kochen, E. P. Specker, “The problem of hidden variables in
quantum mechanics”, Journal of Mathematics and Mechanics. 17 (1): 59–87,
(1967).
[16] W. Wootters, W. A. Żurek, “A single quantum cannot be cloned”, Nature 299, 802–803, (1982).
[17] A. Turing, “Computing Machinery and Intelligence”, Mind, LIX (236): 433–460, (1950).
[18] J. von Neumann, “First Draft of a Report on the EDVAC”, 1945.
[19] R. S. Ingarden, Quantum Information Theory, Reports on Mathematical Physics, vol. 10, 43–72, (1976).
[20] P. Benioff, “The Computer as a Physical System: A Microscopic Quantum Mechanical Hamiltonian Model of Computers as Represented by Turing Machines”, Journal of Statistical Physics, 22, 563, (1980).
[21]. R. Feynman, “Simulating Physics with Computers”, International Journal of Theoretical Physics, 21 (6–7): 467–488, (1982).
[22] D. Deutsch, R. Jozsa “Rapid solutions of problems by quantum computation”. Proceedings of the Royal Society of London A, 439 (1992).
[23] http://www.thomaswong.net, T. Wong, Introduction to Classical and Quantum Computing.
[24] https://magazine.caltech.edu/post/untangling-entanglement
[25] https://royalsocietypublishing.org/doi/10.1098/rspa.1992.0167
[26] https://epubs.siam.org/doi/10.1137/S0097539796300921
[27] https://epubs.siam.org/doi/10.1137/S0097539796298637
[28] https://epubs.siam.org/doi/abs/10.1137/S0036144598347011
[30] R. L. Rivest, A. Shamir, and L. Adleman, “A method of obtaining digital signatures and public-key cryptosystems”, Comm. Assoc. Comput. Mach., 21, pp. 120–126, (1978).
https://dl.acm.org/doi/pdf/10.1145/359340.359342
[31] https://csrc.nist.gov/Projects/post-quantum-cryptography/post-quantum-cryptography-standardization
[32] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.80.3408
[33] https://en.wikipedia.org/wiki/List_of_quantum_processors
[34] https://pennylane.ai/qml/demos/tutorial_trapped_ions
[35] https://pennylane.ai/qml/demos/tutorial_sc_qubitshttps://pennylane.ai/qml/demos/tutorial_sc_qubits
[36] https://pennylane.ai/qml/demos/tutorial_photonics
[37] https://ionq.com/
[38] https://www.aqt.eu
[39] https://www.oxionics.com/
[40] https://www.quantinuum.com/
[41] https://quantumai.google/
[42] https://www.ibm.com/quantum
[45] https://www.psiquantum.com/
[46] https://docs.dwavesys.com/docs/latest/c_gs_2.html
[47] https://www.nature.com/articles/s41534-017-0018-2
[48] https://www.dwavesys.com/
[49] https://www.frontiersin.org/articles/10.3389/fict.2017.00029/full
[50] https://en.wikipedia.org/wiki/Boltzmann_distribution
[51] https://arxiv.org/abs/2110.12408
[52] https://www.sciencedirect.com/science/article/pii/S0304397514004241?via%3Dihub
[53] A. Ekert, “Quantum cryptography based on Bell’s theorem“, Phys. Rev. Lett.67, 661, (1991) https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.67.661
[54] https://www.merton.ox.ac.uk/news/professor-artur-ekert-milner-award
[55] https://www.pcss.pl/nlpqt-uruchomiono-lacze-quantum-key-distribution-miedzy-poznaniem-i-warszawa
[56] https://arxiv.org/abs/1405.4878
[57] W.K. Wooters, W. H. Żurek “A single quantum cannot be cloned”, Nature, 299, 802–803 (1982) https://www.nature.com/articles/299802a0
[58] A. Kossakowski, “On quantum statistical mechanics of non-Hamiltonian systems”, Reports on Mathematical Physics, Volume 3, Issue 4, p. 247–274, (1972).
[59] https://klasterkwantowy.pl
[61] https://qworld.net/qpoland
[62] https://qworld.net
[63] https://www.qaif.org
[64] https://www.qaif.org/events/workshops/qbronze113-19-21-09-25-26-09-2023
[65] https://www.qaif.org/contests/quantum-games-hackathon
Dominik Andrzejczuk
Polish American Venture Capitalist